A hierarchy of simplifying assumptions for grounded ice flow

Table 4 describes a hierarchy of models, listed roughly in order of increasing effectiveness in modeling grounded ice sheets with fast flow features. This is also the order of increasing need for data to serve as boundary and initial conditions, however, as also described in the Table.

Table 4 Hierarchy of flow models in PISM for the grounded parts of ice sheets. Listed from most to fewest simplifying assumptions and from least to greatest need for boundary data. The italicized models are planned for future versions of PISM but are not implemented so far.

Model

Assumptions

Required data

perfectly-plastic ice

steady state; ice has shear stresses below a pre-determined ice “yield stress”; also needs pre-determined location of ice sheet margin

  • bed elevation

balance velocities

steady state; ice flows down surface gradient [57]

same as above, plus:

  • surface mass balance

  • (initial) ice thickness

isothermal SIA

non-sliding lubrication flow, fixed softness [58], [59]

same as above, but time-dependence is allowed

thermo-coupled SIA

non-sliding lubrication flow, temperature-dependent softness [16], [12]

same as above, plus:

  • surface temperature

  • geothermal flux

polythermal SIA

allows liquid water fraction in temperate ice; conserves energy better [22], [44]

same as above

SIA + SSA hybrid

SSA as a sliding law for thermo-coupled SIA [10], [17]; polythermal by default

same as above, plus:

  • model for subglacial water

  • model for basal resistance

First Order Approximation

pressure within the ice is hydrostatic; x and y derivatives of the vertical velocity component are small compared to z derivatives of horizontal components [41], [42], [60]

same as above

It may also be helpful to view the implemented stress balances as PISM software components (C++ classes). Fig. 14 shows the sequences of actions taken by the SIA-only, SSA-only, and SIA+SSA hybrid model components. In each case a membrane stress solution is generated first, then a distribution of vertical shear in the column of ice is generated second, and finally a use of incompressibility computes the vertical component of the velocity. The nonsliding SIA-only model has a trivialized membrane stress solution. The SSA-only model has a trivialized computation of vertical shear.

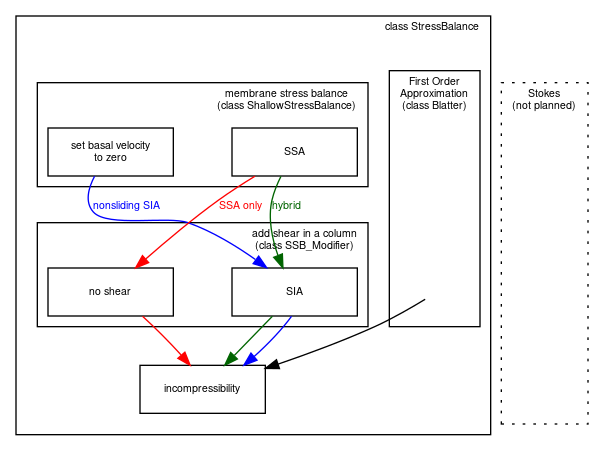
../../_images/stressbalance.png

Fig. 14 The SIA-only, SSA-only, and SIA+SSA hybrid models represent different “routes” through stress balance PISM components. In each case the inputs are ice geometry and boundary stresses, and the final output is a three-dimensional velocity field within the ice.

Previous Up Next